Can Two Obtuse Angles Be Complement to Each Other

Introduction

In the realm of geometry, understanding the relationships between different types of angles is fundamental. Among these relationships, the concept of complementary angles often arises. A common question posed by students and enthusiasts alike is: Can two obtuse angles be complement to each other? This article delves deep into this query, exploring definitions, mathematical reasoning, and practical examples to provide a clear and comprehensive answer.

Understanding Angle Types

Before addressing the main question, it’s essential to grasp the basic types of angles:

• Acute Angle: Measures less than 90 degrees.
• Right Angle: Measures exactly 90 degrees.
• Obtuse Angle: Measures more than 90 degrees but less than 180 degrees.
• Straight Angle: Measures exactly 180 degrees.
• Reflex Angle: Measures more than 180 degrees but less than 360 degrees.

Understanding these classifications sets the foundation for exploring how angles interact, particularly in complementary relationships.

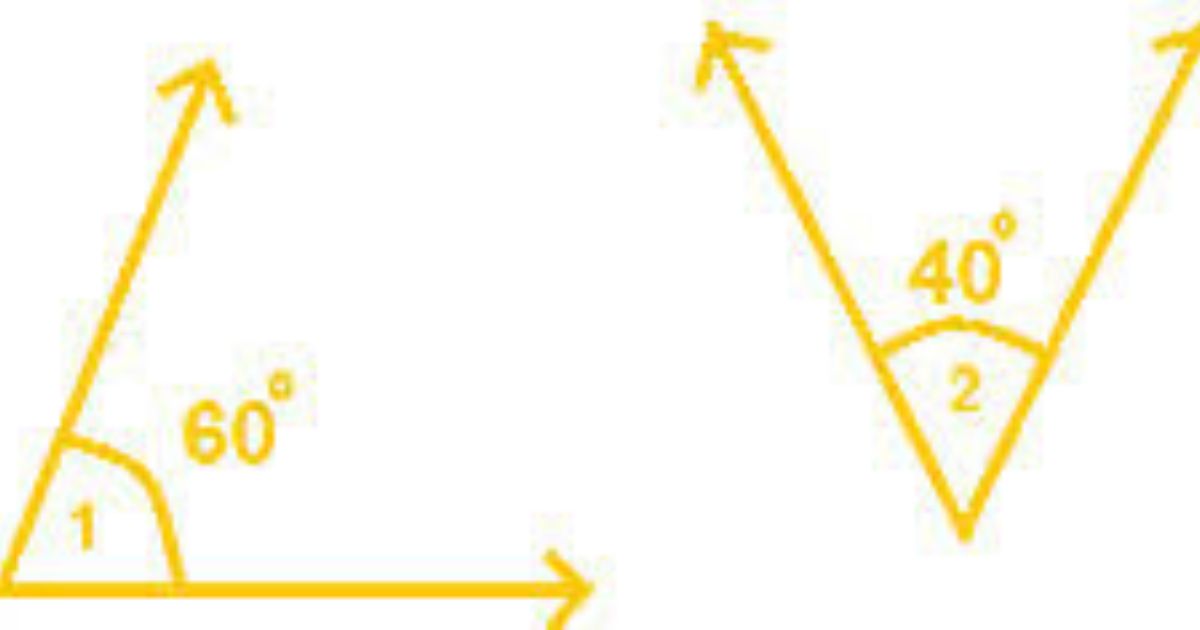
What Are Complementary Angles?

Complementary angles are two angles whose measures add up to exactly 90 degrees. This relationship is pivotal in various geometric constructions and proofs. For instance, if one angle measures 30 degrees, its complement would be 60 degrees, as together they sum to 90 degrees.

Mathematically: If angle A and angle B are complementary, then: Angle A + Angle B = 90°

This definition implies that both angles in a complementary pair must be acute since any angle measuring more than 90 degrees would exceed the total when combined with another angle.

Defining Obtuse Angles

An obtuse angle is one that measures greater than 90 degrees but less than 180 degrees. These angles are wider than right angles and are commonly found in various geometric shapes and real-world structures.

Examples of obtuse angles include:

• 120°
• 135°
• 150°

Given that each of these measures exceeds 90 degrees, they inherently cannot be part of a pair that sums to exactly 90 degrees.

Mathematical Reasoning: Can Two Obtuse Angles Be Complementary?

To determine if two obtuse angles can be complementary, let’s analyze the mathematical implications.

• Let’s assume angle A and angle B are both obtuse.
• By definition, each angle > 90°.
• Therefore, Angle A + Angle B > 90° + 90° = 180°

This sum exceeds 90°, which contradicts the definition of complementary angles. Hence, two obtuse angles cannot be complementary.

This conclusion is supported by authoritative sources. For instance, BYJU’S states: “Two obtuse angles cannot complement each other” . Similarly, Cuemath explains that complementary angles must sum to 90°, making it impossible for two angles each greater than 90° to be complementary .

Common Misconceptions

Misconception 1: Any Two Angles Can Be Complementary

Some believe that any two angles can be complementary as long as their measures add up to 90 degrees. While it’s true that the sum must be 90°, the individual angles must also be less than 90°, i.e., acute. Therefore, two obtuse angles cannot be complementary.

Misconception 2: Complementary and Supplementary Are Interchangeable

Another common confusion is between complementary (sum of 90°) and supplementary (sum of 180°) angles. While two obtuse angles cannot be complementary, they also cannot be supplementary, as their sum would exceed 180°, which is the total required for supplementary angles .

Practical Examples

Example 1: 95° and 100°

• Both angles are obtuse.
• Sum: 95° + 100° = 195°
• 195° > 90°, so they cannot be complementary.

Example 2: 120° and 150°

• Both angles are obtuse.
• Sum: 120° + 150° = 270°
• 270° > 90°, so they cannot be complementary.

These examples illustrate that combining any two obtuse angles will always result in a sum exceeding 90°, thereby disqualifying them from being complementary.

Visual Representation

Imagine a right angle, which measures exactly 90°. To form this angle using two smaller angles, each must be less than 90°. If you attempt to use two obtuse angles, each over 90°, their combined measure would surpass the right angle, making it impossible to form a complementary pair.

Importance in Geometry

Understanding that two obtuse angles cannot be complementary is crucial in geometric problem-solving and proofs. It helps prevent errors in calculations and logical reasoning, ensuring accurate results in constructions and analyses.

Real-World Applications

While the concept may seem theoretical, it has practical implications:

• Architecture: Ensuring structural angles meet design specifications.
• Engineering: Designing components that fit together precisely.
• Art and Design: Creating visually appealing and structurally sound compositions.

In all these fields, recognizing the limitations of angle combinations is essential for success.

Conclusion

Revisiting the central question: Can two obtuse angles be complement to each other? The answer is a definitive no. By definition, complementary angles must sum to exactly 90°, and since each obtuse angle measures more than 90°, their combined measure will always exceed this limit. Understanding this principle is fundamental in geometry and has practical applications in various professional fields.

FAQs

Q1: Can one obtuse angle be complementary to an acute angle?
A1: No. Since an obtuse angle measures more than 90°, adding any positive angle to it will result in a sum exceeding 90°, making it impossible for the pair to be complementary.

Q2: Can two acute angles be complementary?
A2: Yes. Two acute angles can be complementary if their measures add up to exactly 90°.

Q3: Are all complementary angles acute?
A3: Yes. Since their sum is 90°, both angles must individually be less than 90°, making them acute.

Q4: Can two right angles be complementary?
A4: No. Each right angle measures exactly 90°, so their sum would be 180°, which is double the required sum for complementary angles.

Q5: What is the complement of a 60° angle?
A5: The complement of a 60° angle is 30°, as 60° + 30° = 90°.