The study of circles and tangents is a fascinating and foundational part of geometry. When we explore how many tangents can be drawn to a circle, we uncover not only basic geometric properties but also rich applications in higher mathematics, engineering, design, and architecture. In this detailed article, we will thoroughly explore the concept, starting from the basics to advanced understandings, ensuring a comprehensive grasp of the topic.
What is a Tangent?
Before diving into the number of tangents, it is essential to understand what a tangent is. A tangent to a circle is a straight line that touches the circle at exactly one point. This point is called the point of contact. Unlike a chord, which cuts across the circle at two points, or a secant, which passes through the circle, a tangent only grazes the circle.
A key property of a tangent is that it is perpendicular to the radius at the point of contact. In other words, if you draw a line from the center of the circle to the point where the tangent touches, that line will meet the tangent at a right angle (90 degrees).
How Many Tangents Can Be Drawn to a Circle from a Point?
The number of tangents that can be drawn depends on the location of the point relative to the circle. Let’s break it down:
1. Point Outside the Circle
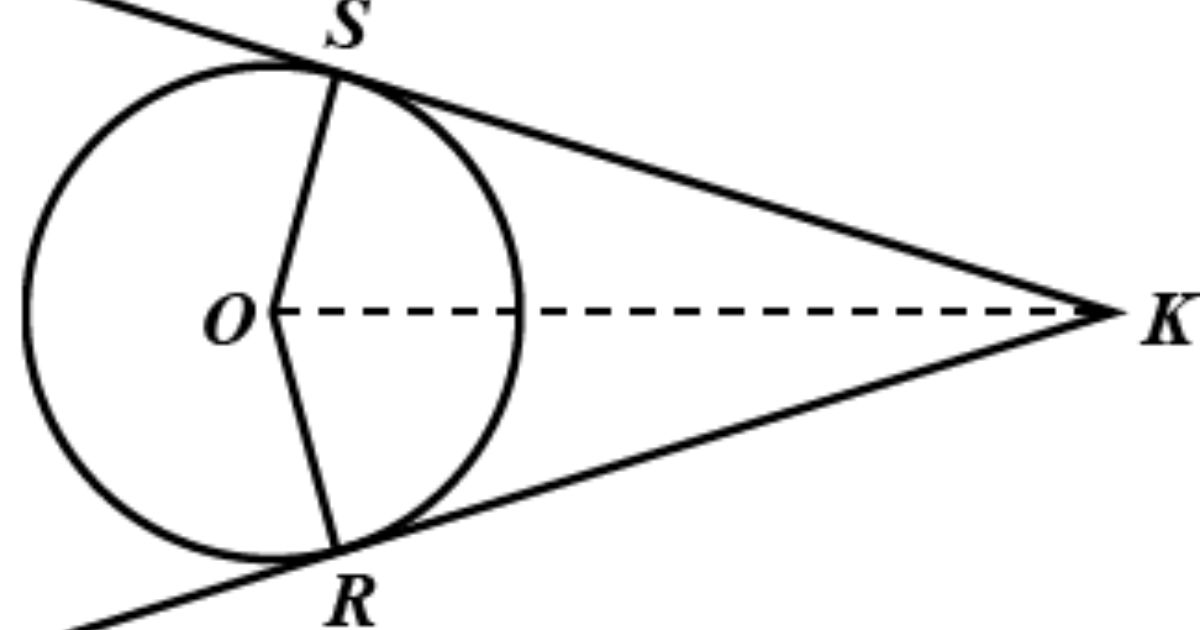
If the point lies outside the circle, exactly two tangents can be drawn to the circle from that point. These two tangents are equal in length.
This is a fundamental result in circle geometry: from any point outside a circle, two unique straight lines can touch the circle exactly once.
Example: Imagine standing a few meters away from a round pond. You could stretch two ropes from your position to just barely touch the edge of the pond at two separate spots without dipping into the water — these are the two tangents.
2. Point On the Circle
If the point lies on the circle, then only one tangent can be drawn. This tangent is perpendicular to the radius at that point.
Example: If you are standing right at the edge of the pond and you stretch a rope in such a way that it doesn’t dip into the pond but just grazes it — that is a single tangent.
3. Point Inside the Circle
If the point lies inside the circle, no tangent can be drawn. Any line you try to draw from this point will either pass through the circle or not touch it at all, but it cannot “just touch” at a single point.
Example: If you are standing in the middle of the pond, you cannot stretch a rope outward that will touch the edge at exactly one point without going through the pond’s water.
Thus, the number of tangents depends critically on where the external point is positioned relative to the circle.
| Location of the Point | Number of Tangents |
|---|---|
| Outside the circle | 2 |
| On the circle | 1 |
| Inside the circle | 0 |
How Many Tangents Can Be Drawn to a Circle Altogether?
If we ask how many tangents can exist in total concerning a circle, without referring to a particular external point, theoretically, there are infinitely many tangents possible.
Each point on the circumference has exactly one tangent, and since a circle has an infinite number of points, an infinite number of tangents exist around a circle.
In simple words:
- From an external point: Maximum two tangents
- Overall: Infinite tangents (because of infinite points on the circumference)
Mathematical Explanation of Tangents
If we want to go deeper into mathematics, we can represent a circle with the equation: x2+y2=r2x^2 + y^2 = r^2
Where (0,0)(0, 0) is the center and rr is the radius.
The general equation of a tangent to this circle can be given as: y=mx±r2(1+m2)y = mx \pm \sqrt{r^2(1 + m^2)}
Where mm is the slope of the tangent. Since mm can vary infinitely (positive and negative slopes), infinitely many tangents are possible.
However, from a fixed external point, solving the system of equations (circle and straight line) results in two possible tangents.
Special Types of Tangents
When studying how many tangents can be drawn to a circle, it’s also essential to consider special types of tangents:
1. Direct Common Tangents
When two circles are separate and do not overlap, direct common tangents are lines that touch both circles externally. Typically, two direct common tangents can be drawn in this case.
2. Transverse Common Tangents
Transverse tangents cross between two circles, touching both from the inside of the combined area.
The number of common tangents depends on the distance between the centers of the two circles and their radii.
| Condition | Number of Common Tangents |
|---|---|
| Circles are separate | 4 |
| Circles touch externally | 3 |
| Circles overlap but do not contain each other | 2 |
| One circle lies inside another | 0 |
Applications of Tangents to Circles
The concept of tangents is not just theoretical — it has real-world applications:
- Engineering: In designing gears, cams, and various mechanical parts where curved surfaces meet straight edges.
- Architecture: Bridges and tunnels often involve tangent lines to arches and domes.
- Physics: Analyzing forces acting tangentially in circular motion problems.
- Computer Graphics: Curves and surfaces are often connected via tangents for smooth transitions.
- Roadway Design: Highways and racetracks use tangents to link curved paths safely.
How to Draw Tangents to a Circle
Here’s a simple method to draw two tangents from an external point:
- Draw the circle and mark the external point (say, P).
- Draw a line joining P to the center of the circle (O).
- Find the midpoint (M) of the line OP.
- Draw a circle with center M and radius equal to MO.
- This new circle will intersect the original circle at two points — label them A and B.
- Draw straight lines from P to A and from P to B. These are the two tangents.
This classical geometric construction ensures accuracy without complicated calculations.
Important Properties of Tangents
Here are some key properties to remember:
- A tangent to a circle is perpendicular to the radius at the point of contact.
- The lengths of two tangents drawn from an external point to a circle are equal.
- The tangent line never enters the circle; it only touches it.
- There can be infinitely many tangents to a circle overall but at most two tangents from an external point.
These properties are often used in geometry problems, proofs, and real-world design considerations.
Example Problem
Problem: A circle has a center at (0,0) and radius 5 units. How many tangents can be drawn from the point (8,6)?
Solution:
First, find the distance between the center and the point: Distance=82+62=64+36=100=10\text{Distance} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10
Since 10 > 5 (the radius), the point lies outside the circle. Therefore, two tangents can be drawn from the point (8,6) to the circle.
Conclusion
Understanding how many tangents can be drawn to a circle provides vital insights into both pure and applied mathematics. From basic school-level geometry to complex real-world structures, the concept of tangents plays a crucial role.
- From an external point, two tangents can be drawn.
- From a point on the circle, only one tangent exists.
- From a point inside the circle, no tangent is possible.
- Overall, an infinite number of tangents can be drawn to a circle when considering all points around its circumference.
This fundamental yet powerful concept is a beautiful example of the elegance and utility of geometry in understanding and shaping the world around us.